Trigonometri2

Introduktion

Den retvinklede trekant er benævnt ABC (bemærk store bogstaver)

Den modstående side til vinkel A er siden |BC| eller a (bemærk lille a)

Den modstående side til vinkel B er siden |AC| eller b (bemærk lille b)

Den modstående side til vinkel C er siden |AB| eller c (bemærk lille c)

Den længste side i den retvinklede trekant har betegnelsen hypotenuse.

Hvis du betragter trekanten fra vinkel A er siden b den hosliggende katete og siden a er den modstående katete.

http://sysform.dk/images/2016/Trigonometri2/image006.png

Hvis du betragter trekanten fra vinkel B er siden a den hosliggende katete og siden b er den modstående katete

Se formlerne i anvendelse under fanebladet eksempler

Eksempler på beregning af længde

Eksempel 1

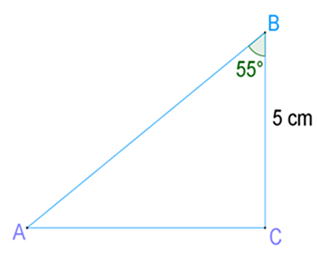
http://sysform.dk/images/2016/Trigonometri2/image010.png

Vi ønsker at finde siden b i trekant ABC

hvor vinkel C er retvinklet

Vi "stiller" os i punktet B og bruger formlen

og indsætter og beregner:

tan(55) = modstående side : 5

tan(55) = 1,428…(fundet på lommeregner)

1,428.. = modstående side : 5

5 ● 1,428... = modstående side

7,1 = modstående side (afrundet til 1 decimal) og dermed længden af b = 7,1 cm

Eksempel 2

Vi ønsker at finde siden c i trekant ABC

Vi "stiller" os i punktet A og bruger formlen

og indsætter og beregner:

cos(23,11) = 6 : hypotenusen

cos(23,11) = 0,92 (afrundet til 2 decimaler)

0,92 = 6 : hypotenusen

hypotenuse ● 0,92 = 6

hypotenuse = 6 : 0,92

6,52 = hypotenusen (afrundet til 2 decimaler) = siden c

Eksempel 3

Vi ønsker at finde siden a i trekant ABC

hvor vinkel C er retvinklet

Vi "stiller" os i punktet A og bruger formlen

og indsætter og beregner:

sin(40,83) =modstående katete : hypotenusen

sin(40,83) = 0,65 (afrundet til 2 decimaler)

0,65 = modstående katete : 6,6

0,65 ● 6,6 =modstående katete

4,32 = modstående katete

siden a er dermed 4,32 cm

Eksempler på beregning af grader

Eksempel 1

http://sysform.dk/images/2016/Trigonometri2/image022.png

Vi ønsker at finde vinkel C i trekant ABC

hvor vinkel A er retvinklet

Vi "stiller" os i punktet C og bruger formlen

og indsætter og beregner:

cos(v) = 4 : 6,02

cos(v) = 0,664…

cos til vinkel C er altså 0,664…

For at finde selve vinkel C benyttes den omvendte funktion til cosinus som betegnes cos ^-1

Funktionen indtastes på lommeregneren og vi får følgende:

C = cos^-1 (0,664) = 48,4⁰ (afrundet til 1 decimal)

Vinkel C er altså 48,4⁰

Øvelse 1.1

Trekantens sider benævnes i disse opgaver som enten a, b, eller c

Hypotenusen i trekanten er siden

Øvelse 1.2

Hvilken side er ∠B's hosliggende katete?

Hvilken side er ∠B's modstående katete?

Siden |BC|hedder også siden

Ret opgaverne

http://sysform.dk/images/2016/Trigonometri2/image030.png

Øvelse 2.1

Vinkel R er 90⁰. Angiv følgende ved brug af sidelængderne r, s og t

http://sysform.dk/images/2016/Trigonometri2/image032.png

sin(T) =

tan(T) =

cos(S) =

sin(S) =

tan(S) =

cos(T) =

Øvelse 2.2

http://sysform.dk/images/2016/Trigonometri2/image034.png

Hvor lang er siden a (svar med 1 decimal)?

Sin(B) = (svar med 2 decimaler)

Cos(B) = (svar med 2 decimaler)

Tan(B) = (svar med 2 decimaler)

Sin(C) = (svar med 2 decimaler)

Cos(C) =(svar med 2 decimaler)

Tan(C) = (svar med 2 decimaler)

Øvelse 2.3

http://sysform.dk/images/2016/Trigonometri2/image036.png

Hvor lang er siden r ?

Sin(R) = (svar med 1 decimal)

Cos(R) = (svar med 1 decimal)

Tan(R) = (svar med 2 decimaler)

Sin(Q) = (svar med 1 decimal)

Cos(Q) =(svar med 1 decimal)

Tan(Q) = (svar med 2 decimaler)

Ret opgaverne

Øvelse 3.1

http://sysform.dk/images/2016/Trigonometri2/image040.png

Vinkel G =

Siden g = ( facit med 1 decimal)

Siden h = ( facit med 1 decimal)

Øvelse 3.2

http://sysform.dk/images/2016/Trigonometri2/image042.png

Vinkel C =

Siden a = ( facit med 2 decimaler)

Siden c = ( facit med 2 decimaler)

Øvelse 3.3

http://sysform.dk/images/2016/Trigonometri2/image044.png

Vinkel K = (facit med 2 decimaler)

Siden l = (facit med 1 decimal)

Siden k = (facit med 1 decimal)

Ret opgaverne